Latent Tree Models
|
A latent tree model, or LTM for short, is a tree-structured Bayesian network with discrete variables.
(There are variants with continuous variables.) The variables at leaf nodes
are observed, and the variables at internal nodes are latent, i.e., not
observed. The root is associated with a marginal distribution, and each of
the other node is associated with a distribution of the node given its
parent. The product of all the distributions defines a joint distribution
over all the variables.
LTMs can be
used for co-occurrence
modelling and for multidimensional
clustering (i.e., the partition
of data in multiple ways using latent variables). ¡¤
Videos: Overview. Lectures: 1 - Basics & Algorithms,
2 ¨C Algorithms &
Applications, 3 ¨C More
Applications. ¡¤
N. L. Zhang, L. K. M. Poon
(2017). Latent Tree Analysis. AAAI2017 Senior Member Track: 4891-4898. ppt ¡¤
N. L. Zhang (2002). Hierarchical latent
class models for cluster analysis. AAAI-02, 230-237. ¡¤
N. L. Zhang (2004). Hierarchical latent class
models for cluster analysis. Journal of Machine Learning
Research, 5(6):697-723, 2004. |
|
|
|
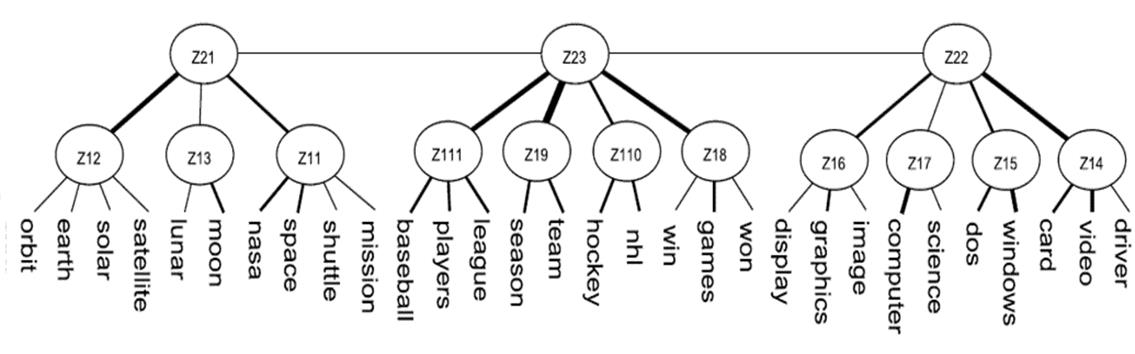
Modelling word co-occurrences: LTMs can be used to model word co-occurrence patterns in documents.
In the example below, the latent variable Z14 indicates the words video,
card, and driver often co-occur in documents; Z15 represents the
co-occurrence of the words dos and windows; Z17 represents the co-occurrence
of image, graphics, display; and so on.
The states of the latent variables represent soft clusters of
documents. They can be interpreted as topics and LTMs are hence used as a novel tool
for hierarchical topic detection , which
significantly outperforms alternative methods. ¡¤
P. Chen, N.L. Zhang, et
al. Latent Tree Models for Hierarchical Topic Detection. Artificial
Intelligence, 250:105-124, 2017. ¡¤
P. Chen, N.L. Zhang, et
al. Progressive EM for Latent Tree Models and Hierarchical Topic Detection. AAAI
2016. ¡¤
T. Liu, N.L. Zhang, P.
Chen. Hierarchical Latent Tree Analysis for Topic Detection. ECML/PKDD (2)
2014: 256-272. ¡¤
Dedicated
Webpage: http://home.cse.ust.hk/~lzhang/topic/ijcai2016/
|
|
|
|
Modelling co-consumption of items: LTM can also be used to model co-consumption of items by users. In the
example below, Z13 indicates that the movies Armageddon, Golden Eye and Con
Air tend to be co-consumed, i.e., watched by the same viewers. Z1148 reveals that the movies Tarzan,
Rugrats, Mulan and Winnie the Pooh tend to be co-consumed.
The states of the latent variables represent soft clusters of users
with different tastes, which are used in a novel method for item
recommendation called conformative filtering. It significantly
outperforms alternative collaborative filtering methods for implicit
feedback. ¡¤
F. Khawar, N.L. Zhang, Y.
Yu. Conformative
Filtering for Implicit Feedback Data. arXiv:1704.01889. |
|
|
|
Modelling co-occurrences of symptoms: LTMs are a natural tool for modelling co-occurrences of symptoms on
patients. The example below is from traditional Chinese medicine (TCM). The left-most part of the model indicates
that the symptoms cold limbs, cold lumbus and back,
intolerance to cold, loose stool tend to co-occurrence. This co-occurrence
pattern corresponds to the TCM concept of Yang Deficiency. The right-most
part of the model indicates that the symptoms yellow urine, thirst, dry
tongue, rapid pulse, tidal fever etc tend to
co-occur. This pattern correspond to the TCM concept of Yin Deficiency.
The work shows that TCM concepts such as Yang
Deficiency and Yin Deficiency are soft patient clusters that can be
identified from clinic data. This is of fundamental importance to TCM because
TCM patient class definitions are subjective and vague. Our work opens up the
perspective of deriving TCM patient class definitions from clinic symptom
distribution data. ¡¤
N. L. Zhang, S. H. Yuan, T. Chen and Y. Wang (2008). Statistical
Validation of TCM Theories. The Journal of Alternative and Complementary
Medicine, 14(5):583-7. ¡¤ Z.X. Xu, N. L. Zhang, et al. (2013). Statistical Validation of Traditional Chinese Medicine Syndrome Postulates in the Context of Patients with Cardiovascular Disease. The Journal of Alternative and Complementary Medicine. 18, 1-6. ¡¤
N. L. Zhang, C. Fu, et al.
(2017). A data-driven method for
syndrome type identification and classification in traditional Chinese
medicine. Journal of Integrative Medicine, 15(2):110¨C123. ¡¤
Dedicated Webpage: http://www.cse.ust.hk/~lzhang/tcm/
|
|
|
|
Modelling co-occurrences (correlations) in survey
data: The model below is learned from data
from a survey about the Danish beer market. According to the model, people's
view about Carlseberg and Groun
Tuborg are strongly correlated. This makes sense
because those are the two main market beers in Denmark. The group in the
middle, CarlsSpec, Tuborgclass
and Henneken are also frequent beers, but they are
darker in taste as compared with the group on the right. The group on the
left are local beers.
The states of the latent variables
identify customers with different preferences and opinions. They are useful
when making marketing strategies. ¡¤ R. Mourad, C. Sinoquet, N. L. Zhang, T.F. Liu and P. Leray (2013). A survey on latent tree models and applications. Journal of Artificial Intelligence Research, 47, 157-203 , 13 May 2013. doi:10.1613/jair.3879 |
|
|
|
Multidimensional Clustering: Clustering is a data
analysis approach where the objective is to find `naturally occurring'
groups. Early research work on clustering usually assumed that there was one
true clustering of data. This assumption does not hold for complex data which
are typically multifaceted and can be meaningfully clustered in many
different ways. There is a growing interest in methods that produce multiple
partitions of data with each partition being based on a different subset of
attributes. We call such methods multi-partition clustering methods.
Analyzing data using
LTMs can result in multiple discrete latent variables, each representing a
soft partition of data. So LTMs can be used for multi-partition clustering. This potential
was first pointed out in (Zhang 2002, 2004). Because latent variables can be
viewed as latent attributes of data, we sometimes call LTM-based cluster
analysis multidimensional clustering. ¡¤
T. Chen,
N. L. Zhang, T. F. Liu, Y. Wang, L. K. M. Poon (2012). Model-based multidimensional clustering of categorical data. Artificial Intelligence.
176(1), 2246-2269. ¡¤
T.F, Liu, N. L. Zhang, P. X. Chen, A. H.Liu, L. K. M. Poon, and Yi Wang (2013). Greedy
learning of latent tree models for multidimensional clustering. Machine Learning, doi:10.1007/s10994-013-5393-0. ¡¤ L. K. M. Poon, N. L. Zhang, T. Chen, and Y. Wang (2010). Variable selection in model-based clustering: To do or to facilitate. ICML-10. ¡¤
L.K.M. Poon, N.L. Zhang, T.F. Liu, A.H. Liu (2013). Model-Based
Clustering of High-Dimensional Data: Variable Selection versus Facet
Determination. International Journal of Approximate
Reasoning. 54(1), 196-215 |
|
|
|
A link to Deep Learning: Hierarchical latent tree models (HLTM) and deep belief networks
(DBNs) are similar in that they both define a distribution over a set of
observed variables and they both use multiple layers of latent variables. On
the other hand, there are obvious differences. One is tree-structured and
learned from data, and the other is fully connected and manually specified.
Those are two extremes.
It would be interesting to explore the
middle ground between the two extremes. One idea is to first learn an HLTM
from data, use it as the skeleton for a deep model, and add additional links
to improve model fit. ¡¤
Z. Chen, N. L. Zhang, et al.
(2017). Sparse
Boltzmann Machines with Structure Learning as Applied to Text Analysis.
AAAI 2017: 1805-1811 |
|
|
|
Code: ¡¤
HLTA: https://github.com/kmpoon/hlta
Use of latent tree models for hierarchical topic detection. ¡¤
Lantern: http://www.cse.ust.hk/~lzhang/ltm/softwares/Lantern.zip
LTM GUI mainly for TCM research. ¡¤
BI: http://www.cse.ust.hk/~lzhang/ltm/softwares/BI.zip
code for Liu et al. (MLJ 2013). ¡¤
EAST: http://www.cse.ust.hk/~lzhang/ltm/softwares/EAST.zip code for Chen et al. (AIJ 2012). |